Java
Oriented
Matroids
Jeremy J. Carroll
Summary
This open source library allows for the creation and manipulation of oriented matroids with high quality code; extensive support for pseudolines, and pseudolines diagrams is provided.
It principally covers the cryptomorphic representations of oriented matroids, allowing seamless conversion between them.
Please contact me if you are using this library.
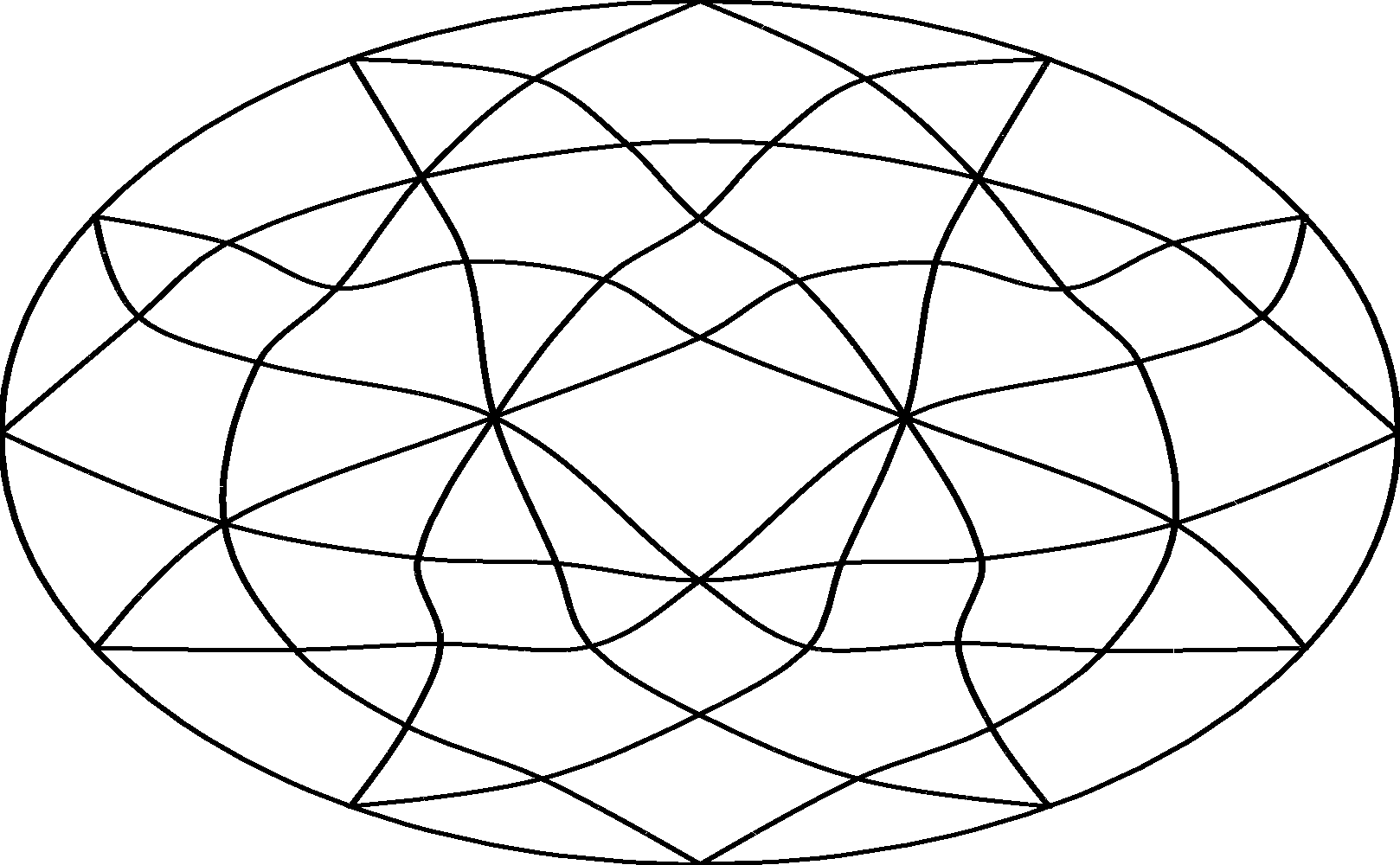
Pseudoline Diagrams
The code comes with several examples built-in of interesting rank 3 oriented matroids. By the topological representation theorem such matroids (or more precisely some reorientation) can be drawn as an arrangment of pseudolines. Traditionally, these arrangements are drawn in in the projective plane. We take such diagrams and project onto the Euclidean plane, mapping one of the pseudolines to the line at infinity, which we represent as an oval.
A good place to start is this one, which has extensive documentation to explain the conventions in the diagram. This is the first example from the Oriented Matroid book. It is strongly recommended that you read this book, and keep it as a reference, when using the Java Oriented Matroid library. That page explains how to read the diagrams, in particular, to understand what 'oriented' means in terms of these diagrams, and the meaning of the origin in this pictures. Since that example is on six elements, there are six slightly different projections onto the Euclidean plane.
More interesting examples are as follows:
| Classical Line Arrangements: | Pappus (c340CE) | Ceva (1678) | ||
|---|---|---|---|---|
| Uniform Variations of Above: | Ringel (1956) | Carroll (2000) | ||
| Arrangements with disconnected realization spaces: | Suvorov (1988) | |||
| Richter-Gebert (1996): | Plus (disconnected) | Zero | Minus (non-realizable) | |
| Tsukamoto (2012): | Plus | Zero | Minus | |
Developer Documentation
The on-line javadoc is the guide to the API. This includes programmatic access to the examples seen above.
Sourceforge Links
Difficulties in Being Straight
The primary goal is to help me on my long-term project concerning pseudoline stretching.
The fundamental approach is essentially the same as in my technical report from 2000, significantly updated with an oriented matroid viewpoint, as described in too much length in A New Proof of Pappus's Theorem:
- Convert to polar co-ordinates
- Find slope constraining sub-arrangements
- Express the slope constraint of each sub-arrangement
-
Simultaneously solve the slope constrains.
- If insoluble:
- Convert constraints into a final polynomial
- If soluble:
- Create linear program for the r co-ordinates
- solve that program
With release 0.3 of September 2013, the prerequisite work on oriented matroids is sufficiently complete, and the system draws pseudoline diagrams: the next release will include some of the implementation of this realizability algorithm (for rank 3 oriented matroids)
Acknowledgement
Many thanks to YourKit Java Profiler, which we whole-heartedly recommend.