Home⇨

The omega14⁻ oriented matroid

Richter-Gebert, [1996] presents two oriented matroids, both derived from a third. His title, two interesting oriented matroids, suggests he sees the third one as dull — we include it nevertheless. The basic derivation is from this matrix:

A B C D E F G H I J K L M N
1 0 1 0 1 1 2 3 2 3 1 1 -1 0
0 1 0 1 1 2 1 2 3 1 3 -1 1 0
0 0 1 1 2 2 2 4 4 4 4 4 4 1

This oriented matroid is defined with a chirotope being the 3 by 3 determinants of the above matrix except that:

χ(L,M,N) = −1

This oriented matroid is interesting, because, like Ringel's it is not realizable, but in addition, the method of proving its non-realizability by finding a biquadratic final polynomial does not work.


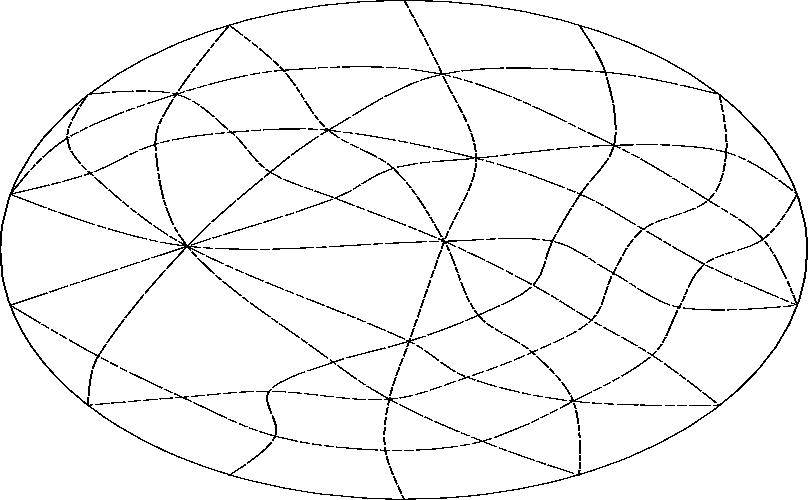
With line A projected to infinity.

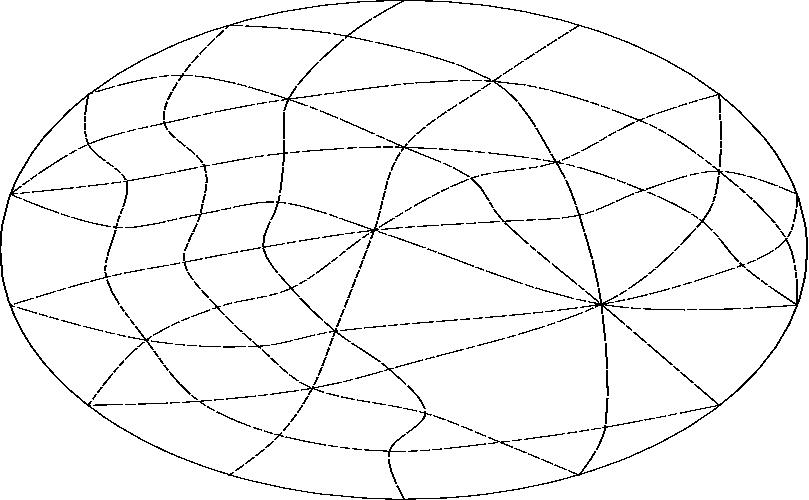
With line B projected to infinity.

With line C projected to infinity.

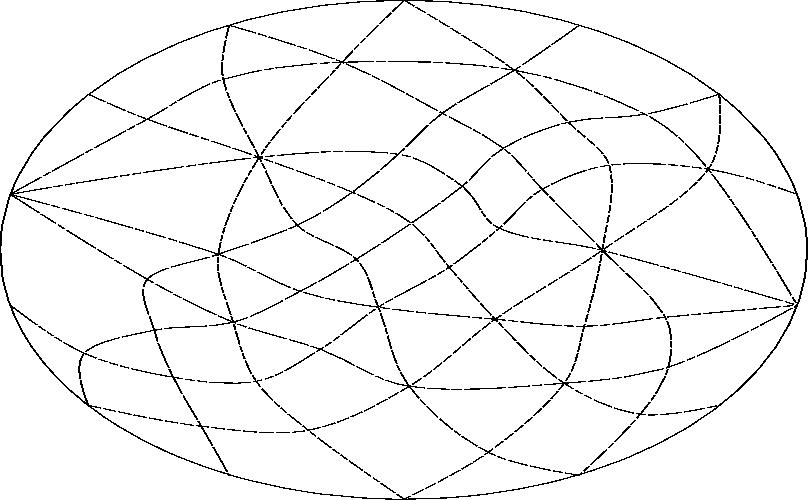
With line D projected to infinity.

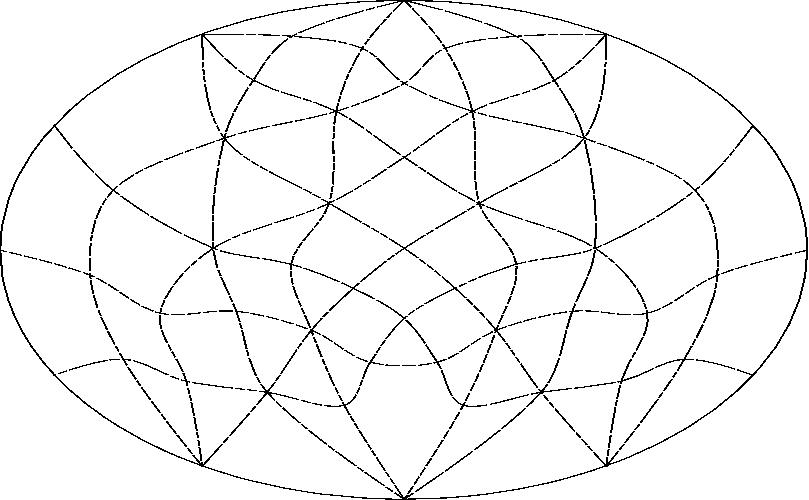
With line E projected to infinity.

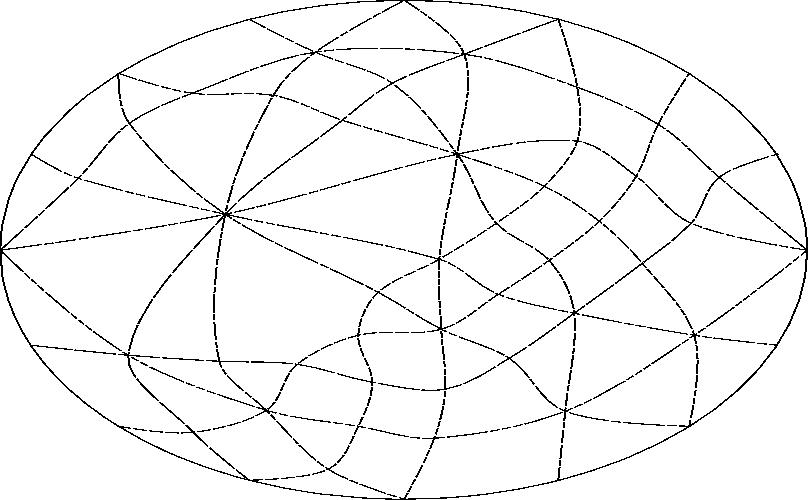
With line F projected to infinity.

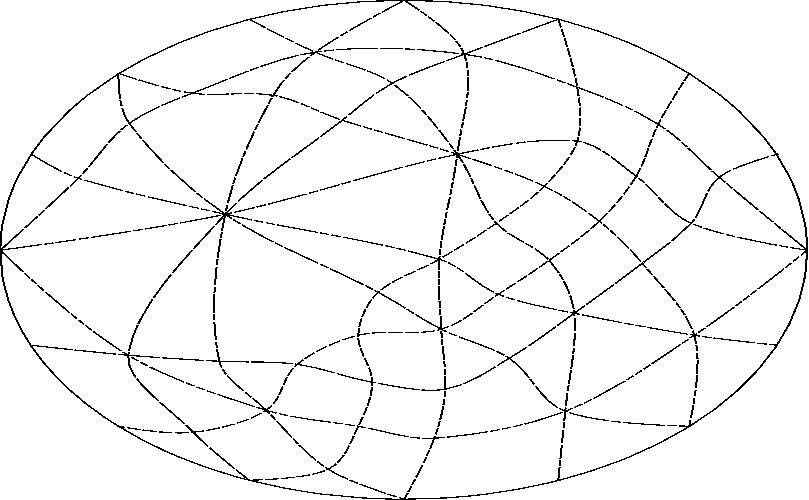
With line G projected to infinity.

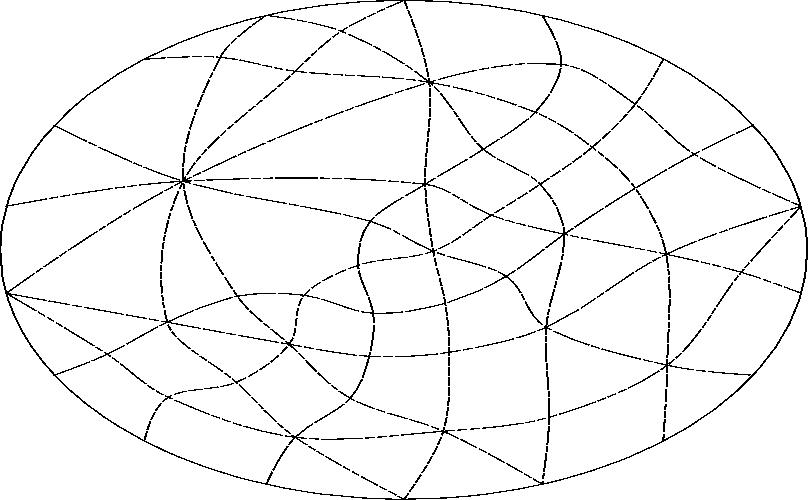
With line H projected to infinity.

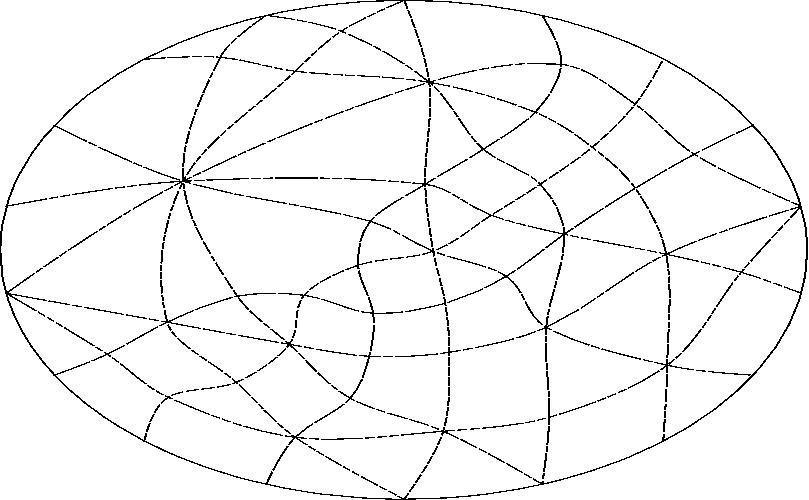
With line I projected to infinity.

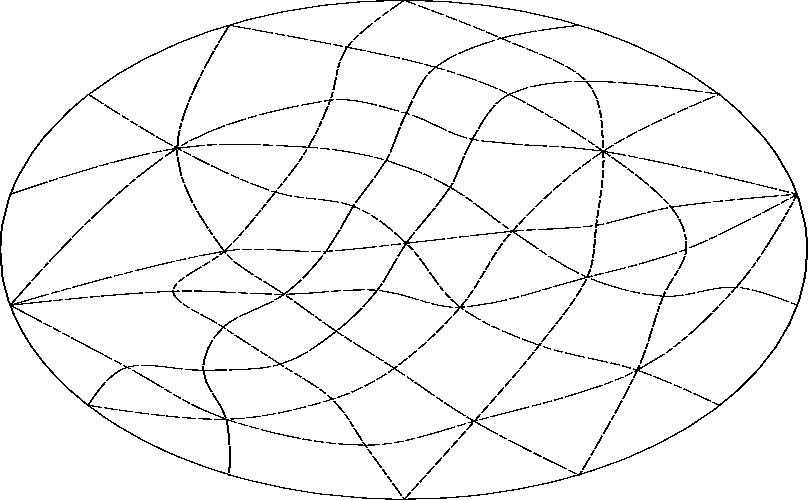
With line J projected to infinity.

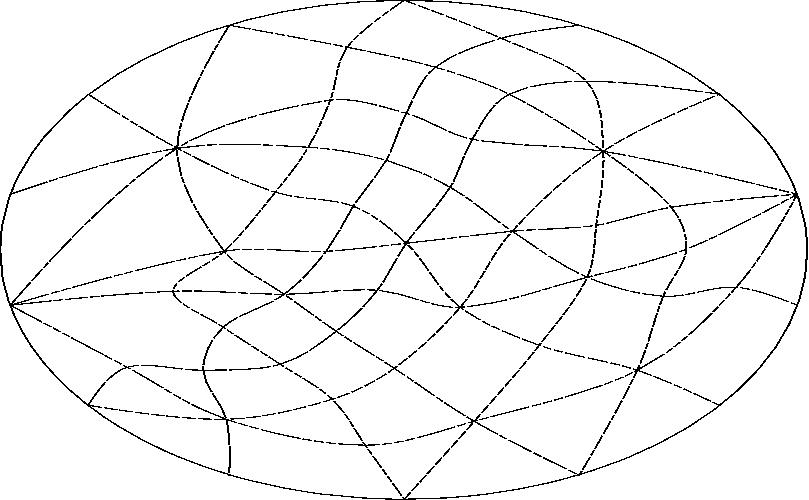
With line K projected to infinity.

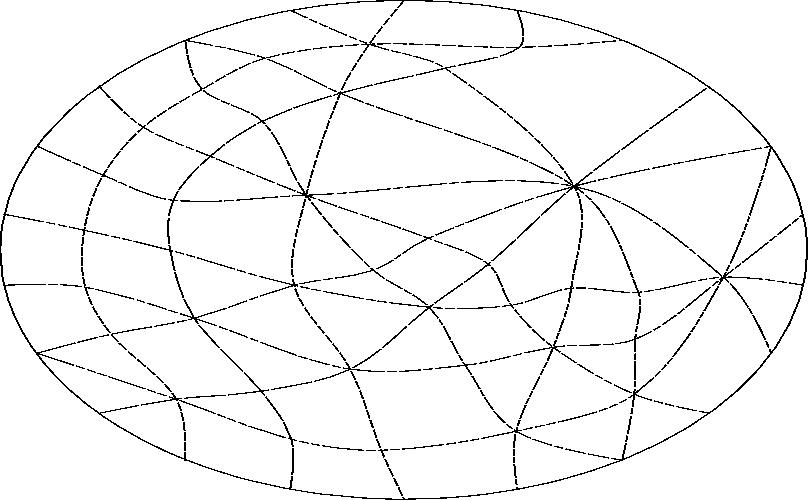
With line L projected to infinity.

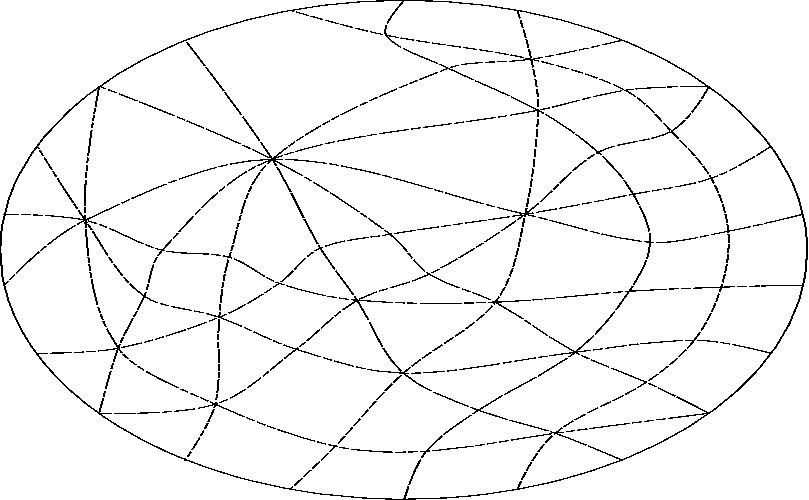
With line M projected to infinity.

With line N projected to infinity.