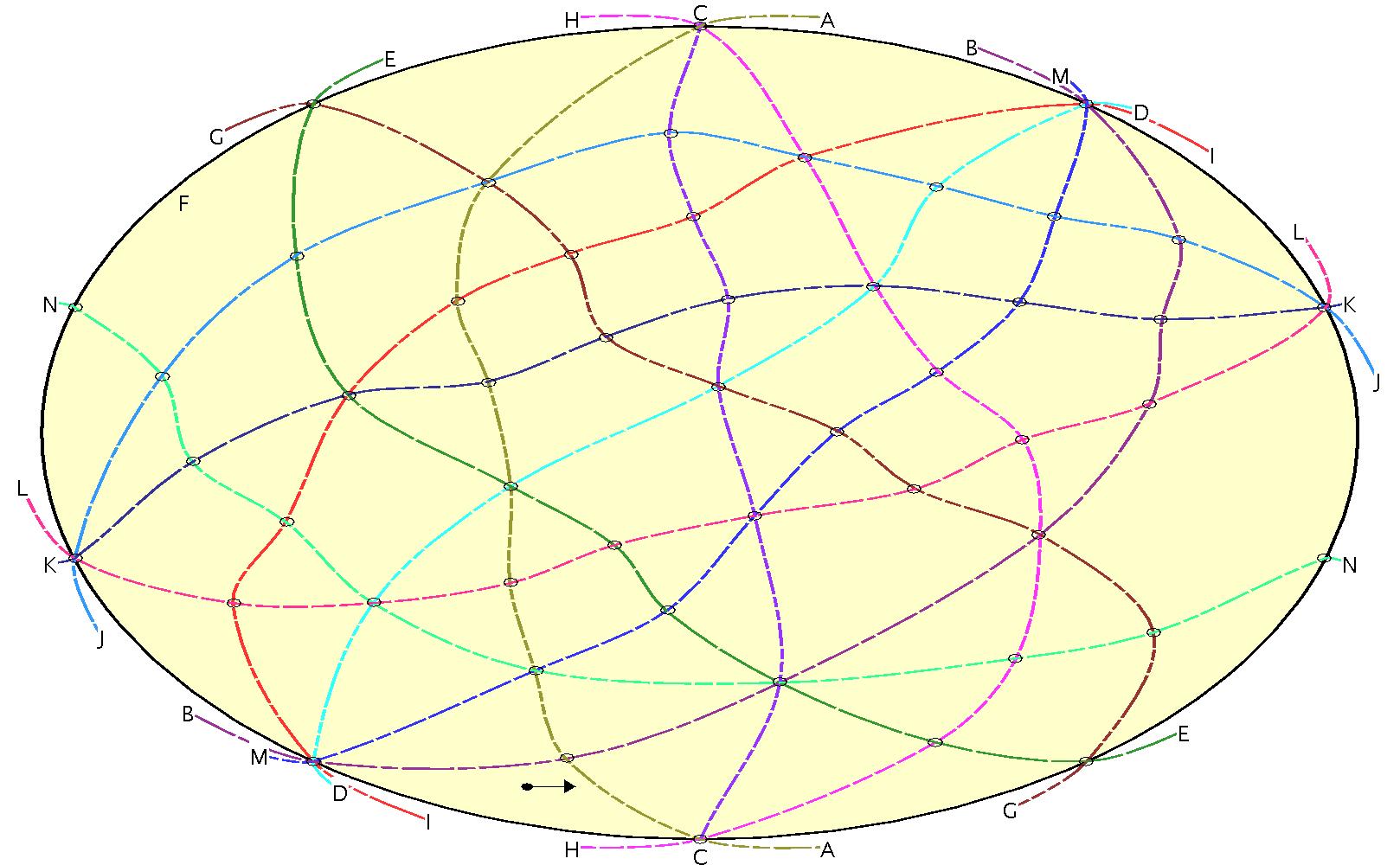
Suvorov, [1988] presents this oriented matroid, which was the first shown to have a disconnected realization space. That means that there are two different realizations of this pseudoline arrangement as equivalent line arrangements, such that it is not possible to continuously transform one to the other through a sequence of equivalent line arrangements.
The oriented matroid is defined by the 3x3 subdeterminants of the following matrix, with s=1.780776 and t=3.936742 (approximately); the alternative realization has s=1.780776 and t=5.186363.
| A | B | C | D | E | F | G | H | I | J | K | L | M | N |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | s | 2*s | 2*s+ 1 | -2*s | 2*s | t - s - 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | s+ 1 | 3*s+ 1 | 2*(s+1) | t-3*s-1 | 3*s-t+ 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 2 | 2 | s+ 1 | 4*s | 3+2*s | t-4*s | 3*s-t+ 1 | s - 1 |
The oriented matroid as presented above is cyclic and does not have a positive face, therefore, to draw a Euclidean pseudoline arrangement which has a positive face we always need to reorient at least one element, equivalent to multiplying the columns named below by −1.
A, L
H, C, A< G, E< N< J, K, L< I, D, M, B