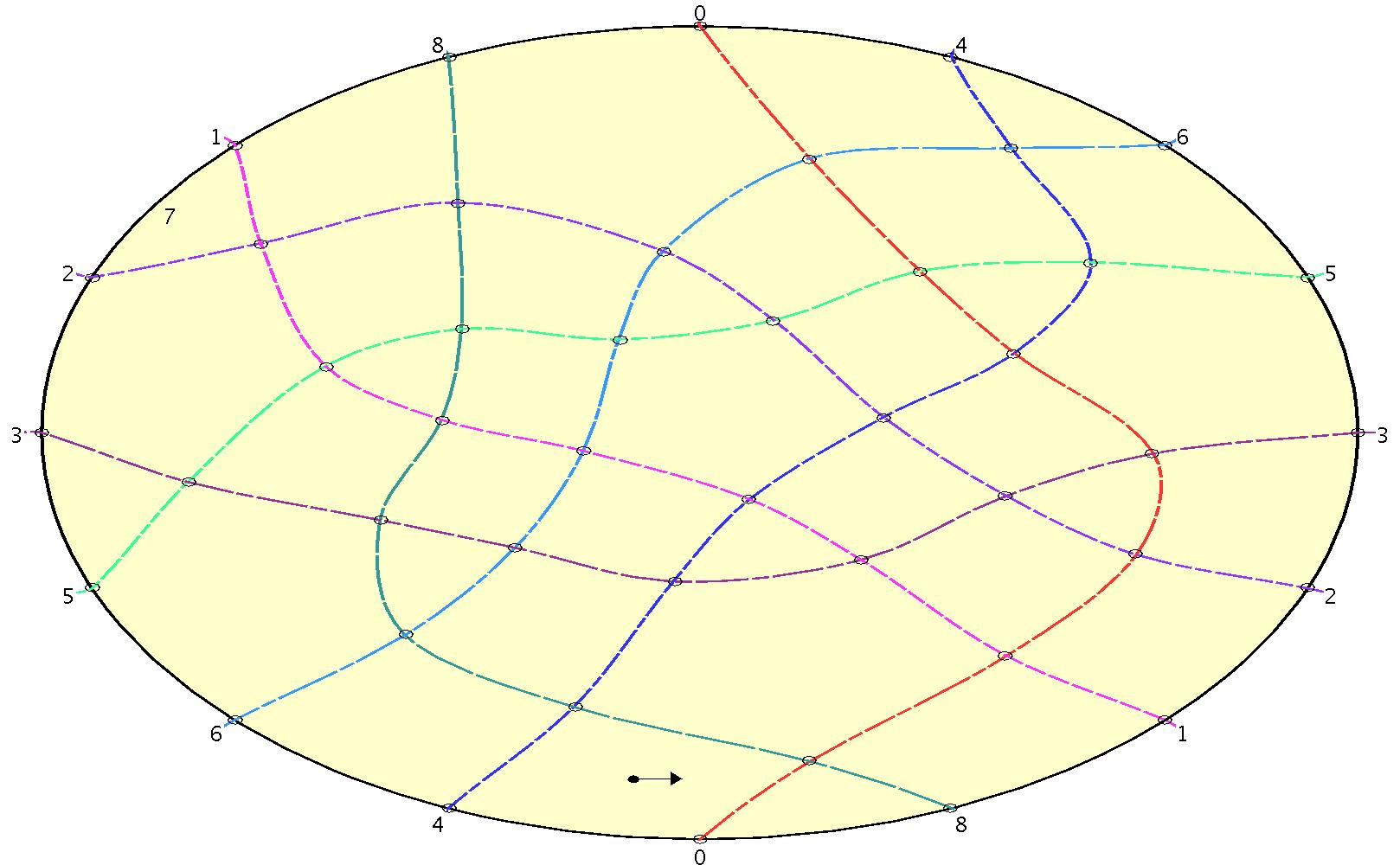
Ringel's oriented matroid is the unique non-realizable rank 3 oriented matroid on 9 elements. Ringel [1956] introduced it as a deformation of Pappus's line arrangement, using a picture. Grünbaum [1969] greatly improved the picture as this:

Our pictures look quite different — one of the main reasons being that we show one of the nine lines as the line at infinity. As a non-realizable arrangement, there are no equivalent arrangement of lines (in the projective plane) equivalent to the arrangement of nine pseudolines. This means that, discarding the line at infinity and viewing each of our pseudoline arrangements as eight pseudolines in the Euclidean plane, we cannot make them straight, whereas, in the projective plane, the arrangements are necessarily stretchable.