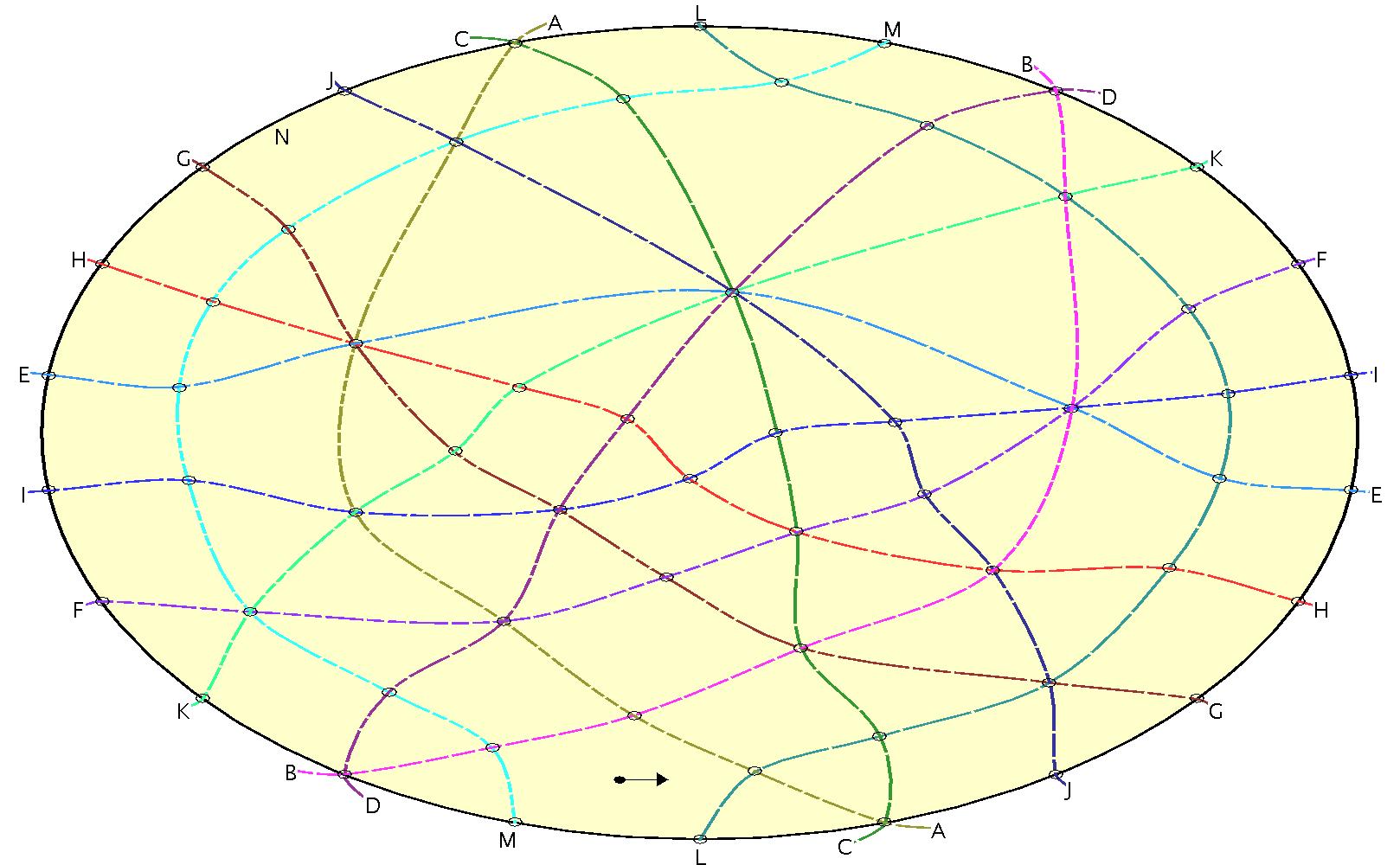
Richter-Gebert, [1996] presents two oriented matroids, both derived from a third. His title, two interesting oriented matroids, suggests he sees the third one as dull — we include it nevertheless. The basic derivation is from this matrix:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 | 1 | 2 | 3 | 2 | 3 | 1 | 1 | -1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 2 | 1 | 2 | 3 | 1 | 3 | -1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 2 | 2 | 2 | 4 | 4 | 4 | 4 | 4 | 4 | 1 |
This oriented matroid is defined with a chirotope being the 3 by 3 determinants of the above matrix except that:
This oriented matroid is interesting, because like Suvorov's one, its realization space is disconnected. It is also easier to define, using only integers in the matrix.
L< C, A< J< G< H< E< I< F< K< D, B< M