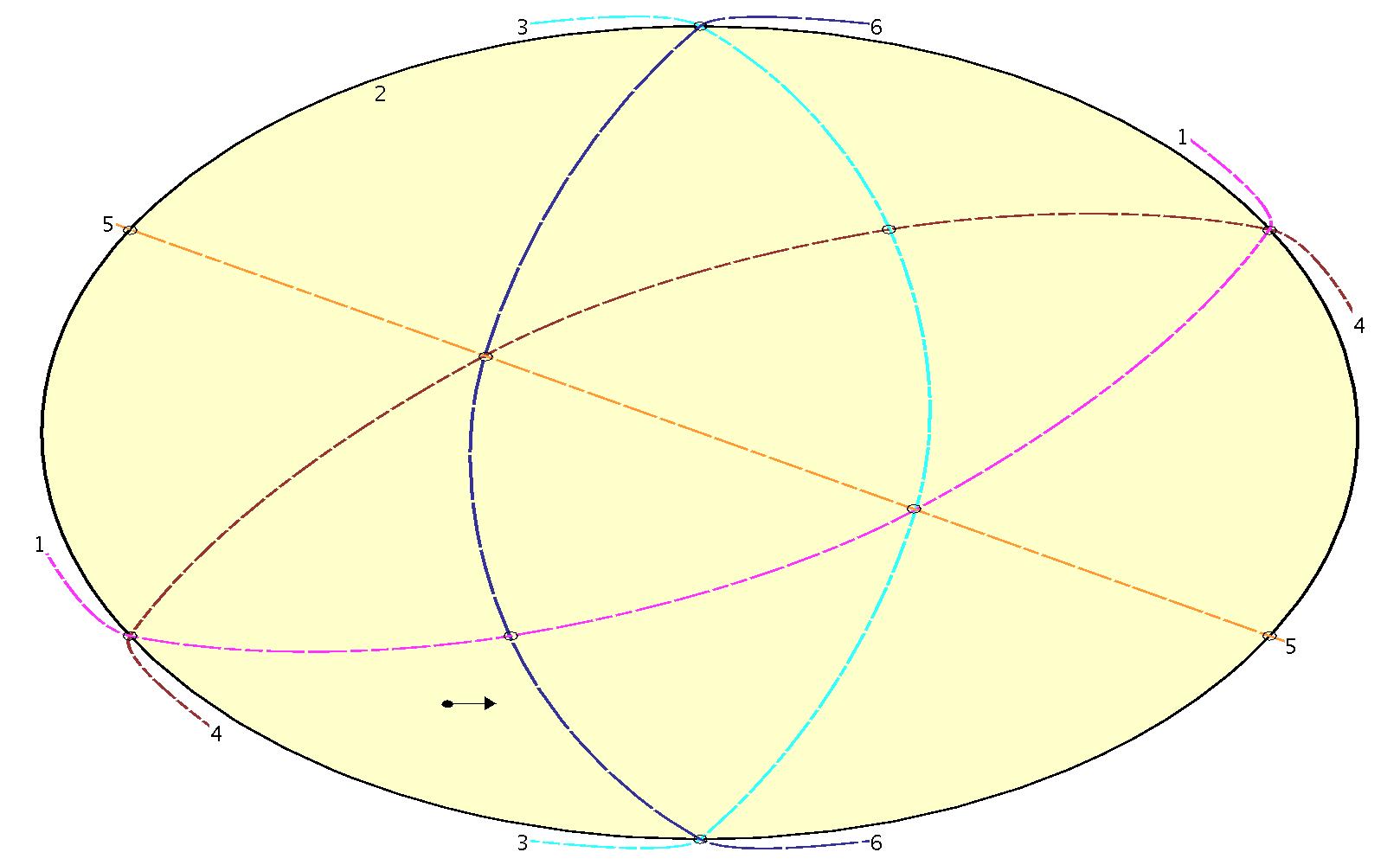
This Oriented Matroid is the introductory example from Oriented Matroids
by
Björner, Las Vergnas, Sturmfels, White and Ziegler, [1999].
One of the ways in which they describe it, is with the following picture:
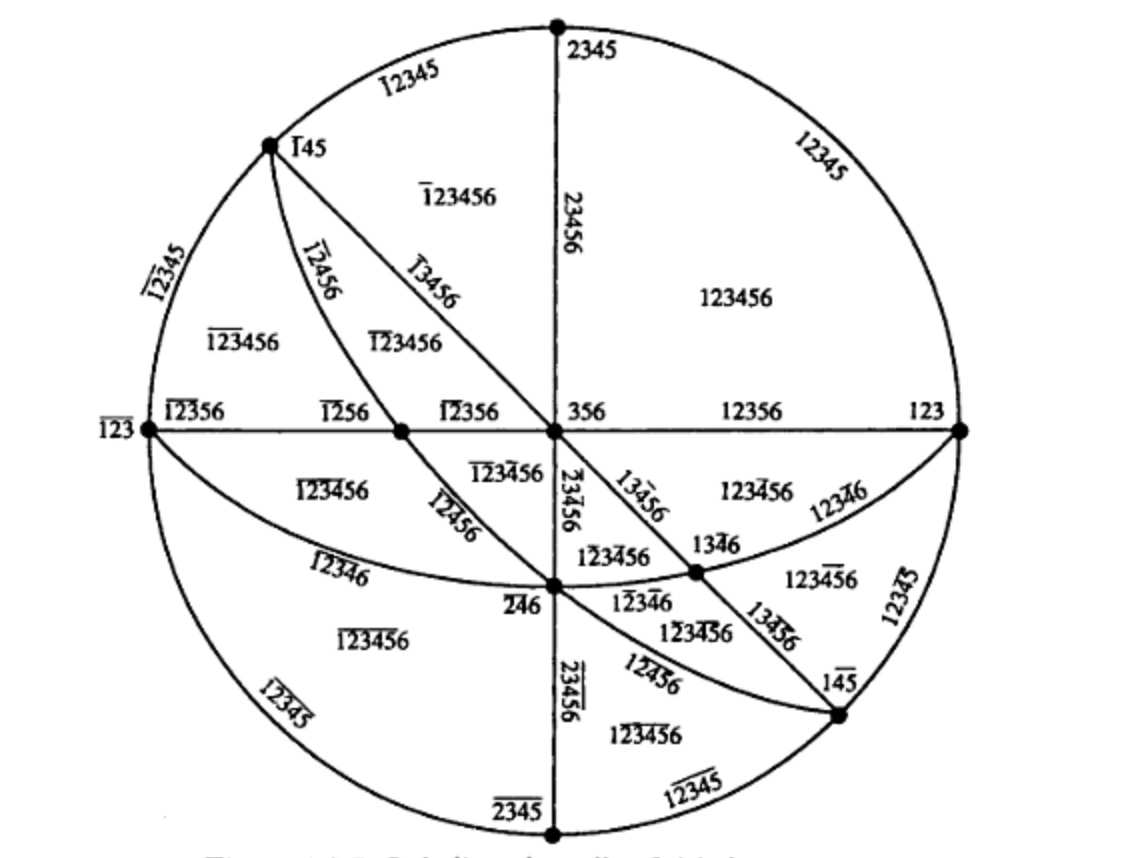
This is essentially the same picture as our sixth projection.
They also define it in terms of the positively and negatively oriented bases. The orientation of a basis depends on the order in which the elements are considered. In each of our projections, we consider the elements as ordered, first: the element projected to infinity, and then the other elements in order going along the line at infinity. This differs from their ordering (which is 1, 2, 3, 4, 5, 6). Hence, depending on the parity of the number of swaps of ordering, we may agree or disagree with their definition of the orientation of a particularly basis.
In addition, we show the orientation of a basis which includes the line projected to infinity simply by the ordering along the line at infinity.
In Björner et als. presentation of this matroid, in its original orientation, they have the following posivie bases:
123, 125, 126, 136, 145, 146, 156, 245, 246, 256, 345, 346, 356
And the following negative bases:
134, 234, 235
Line 2 in the picture above does not directly border onto the positive face (it does touch the face at a point). Our convention of always placing the origin in a face bordering the line at infinity (i.e. an unbounded face) leaves us with a problem when we wish to project line 2 to infinity. We resolve that problem by reorienting the matroid by flipping the orientation of pseudoline 1. With this change, as below, we can label a face with the origin since it is the positive face in the reoriented matroid, and it does border line 2. Any basis which includes line 1 is flipped from positively oriented to negatively oriented (or conversely).
1
3, 6< 5< 4, 1