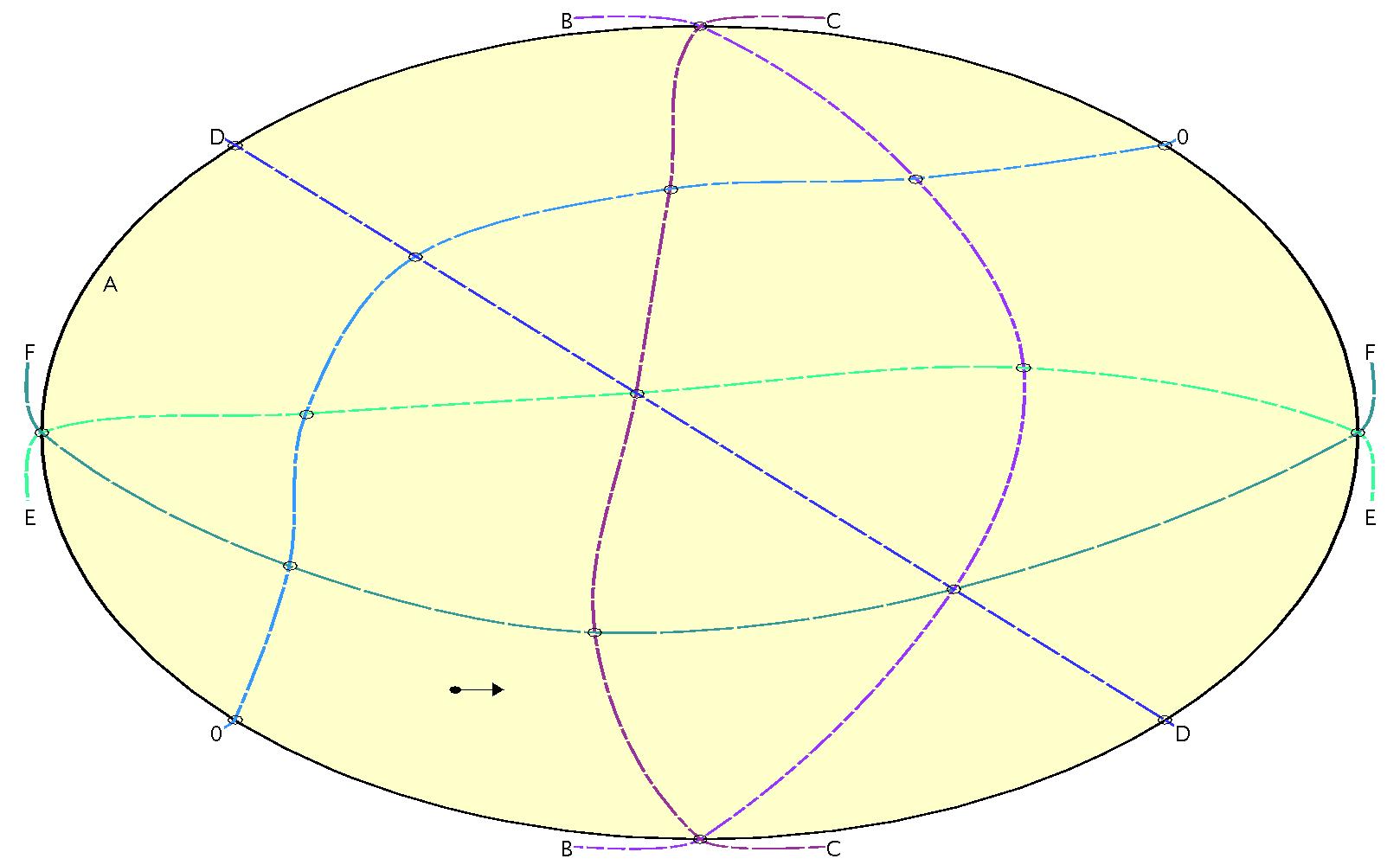
Ceva [1678]'s theorem concerning six lines intersecting in four points is interesting as an early example of a slope constraint. Ringel [1956]'s conjecture that there are no slope constraints on line arrangements in general position is not directly contradicted by this, but a deformation of Ceva's construction, following the approach of Ringel's own deformation (in the same paper) of Pappus' line arrangement, is enough to disprove the slope conjecture.
Slope constraints are important in Oriented Matroid theory because they relate to concerns such as realizability and the topology of realization spaces.
Ceva's theorem is set in the Euclidean plane, not the projective plane, so to map into the Oriented Matroid world, we need to add a seventh line, the line at infinity, which is line 0 in our construction. Thus projecting line 0 to infinity gives Ceva's own arrangement, for which we have the slope constraint:
sin(θF-θE)sin(θD-θC)sin(θB-θA) = sin(θF-θA)sin(θE-θD)sin(θC-θB)
Where θF is the angle in polar co-ordinates of line F.
This relationship between products of sines of differences of angles is a very typical slope constraint.
B, C< D< E, F< 0